Scale, Spatial Data Aggregation, Dasymetric Mapping
This week I completed the final lab for GIS 5935 which focused on scale, spatial data aggregation, and dasymetric mapping. Here I learned about the effects of scale on vector data and resolution on raster data. In addition, we covered the effect of the Modifiable Area Unit Problem (MAUP) while using regression analysis, also known as ordinary least squares (OLS) analysis. I also learned how to identify multipart features and measure compactness.
For the first part of the lab I examined the effect of scale on vector data, in this case hydrographic polyline and polygon features from Wake County, North Carolina. Understanding the meaning of scale is important in GIS, especially how this effects resolution and extent (Goodchild 2011). I found in my analysis that the larger the scale, the increased length of polylines, perimeter lengths, area, and number of polygons. Regarding vector data, resolution can be difficult to define and if possible it is best to use raster data for this purpose (2011).
For the next part of the assignment, I examined the effects of resolution on raster data with a focus on a small coastal watershed in California. Regarding the effect of resolution on raster data, the grid cell size of a raster digital elevation model (DEM) will have significant effects on variables derived from, for example, terrain analysis such as slope, aspect, plan, and profile curvature or the wetness index (Kienzle 2004). For the assignment, I used the Resample tool in ArcGIS to determine the relationship between resolution and average slope through a set of DEMSs I created in varying resolutions: 1, 2, 5, 10, 30, 50, and 90 meters. In this tool, I used the Bilinear interpolation technique which helps determines the new value of a cell based on a weighted distance average of the four nearest input cell centers. It is useful for continuous data and will cause some smoothing of the data.
For the last part of the lab, I used GIS to analyze the relationship between poverty and race for different geographic units in the context of legislative redistricting. As part of this exercise, I considered the Modified Area Unit Problem (MAUP), which is a “serious analytical issue for analysts using spatial data” (Manley 2014:1157). During the process of aggregating spatial data, the results are conditioned by the scale at which this takes place and the ways we configure areal units (2014). It is a problem that Manley writes “will never be truly resolved” although a limited set of solutions have been proposed for just a few cases (2014). For the task assigned, I conducted a comparative analysis via OLS on four different units of analysis: original block groups, zip codes, house voting districts, and counties. I found that the variables associated when measured via counties and block groups have a higher correlation than zipcodes or house voting districts.
Other tasks in this lab included evaluating the shape and compactness of United States congressional districts. Here I selected only those districts encompassing the continental U.S.A. Out of a total of 444 congressional districts, 435 met this criteria. Compactness refers to the area that a feature, such as a congressional district, occupies in relation to its center area (Morgan and Evans 2018). Compactness can be measured through the Polsby-Popper score, which is a geometric formula that compares area, A, to perimeter, P, which is expressed as:
Essentially, the lower the P-P score, the less compact the unit of analysis is. By using the Calculating Geometry tool, I was able to identify the "worst offenders", which were those districts that were the least compact as evidence by the lowest P-P score. The worst offender was Congressional District 12 in North Carolina, with a P-P score of 0.029. The image below shows the shape of this district:
In
contrast, the most compact district, which had the highest P-P score,
was the Congressional District (at large) for Wyoming, at 0.77. This is basically the entire state of Wyoming, and the high level of compactness is not surprising given its relatively rectangle-like shape:
An important concept to consider through this study is gerrymandering, which refers to drawing a district with intentional bias, where one political party will benefit over another (Morgan and Evans 2018).
Overall, I found the final lab assignment interesting and helpful in not only introducing me to some new tools and techniques that I was unaccustomed to, but also reinforcing pre-existing knowledge. I especially enjoyed completing the last part of the lab, because it touches on some of the issues in the social sciences I am already familiar with. As part of my background is in the field of sociology, gerrymandering is a common topic addressed by the discipline and often part of larger discussions about race/ethnicity, power, politics, and geography. This was a good exercise to end the class with because this provided me with some good insights into some of the more technical and geographic aspects of gerrymandering.
2011 Goodchild, Michael F.
"Scale in GIS: An Overview." Geomorphology 130:5-9.
2004 Kienzle, Stefan
"The Effect of DEM Raster Resolution on First Order, Second Order and Compound Terrain Variables." Transactions in GIS 8(1):83-111.
2014 Manley, David
"Scale, Aggregations, and the Modifiable
Areal Unit Problem." In Handbook of Regional
Science, M.M. Fischer, P. Nijkamp,
eds.
2018 Morgan, J.D. and J. Evans.
"Aggregation of Spatial Entities and Legislative Redistricting." The Geographic Information
Science & Technology Body of Knowledge, 1st Quarter Edition, John P. Wilson, ed.
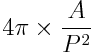


Comments
Post a Comment